Relations and Functions :

1. Let Z be the set of all integers and R be the relation on Z defined as R = {(a, b) : a, b Z, and (a - b) is divisible by 5}. Prove that R is an equivalence relation.

2. Show that the relation S in the set R of real numbers, defined as is neither reflexive, nor symmetric, nor transitive.

3. Show that relation R in the set of real numbers, defined as R = is neither reflexive nor symmetric nor transitive.

4. Show that the funtion defined by is neither one-one nor onto. Also, if is defined as g(x) = 2x - 1, find fog (x).

5. Consider given by f (x) = . Sow that f is invertible with

6. If f (x) = show that f 0 f (x) = x for all . what is the inverse of f ?

Inverse Trigometric Functions :

7. If prove that

8. If then find the value of x.

9. Prove that 2

10. Find the value of

11. Prove that .

12. Prove that

Determinants :

13. Using properties of determinants, prove that .

14. If = 0, then show that 1 + xyz = 0.

15. Using the properties of determinants, prove that

16. If = 0, find the value of

17. Prove that

Matrics :

18. Solve the following system of equations, using matrix method : x + 2 y + z = 7, x + 3 z = 11, 2 x - 3 y = 1

19. Use the product to solve the following system of equations :

20. If A = , find and hence solve the system of linear equations. x + 2y + z = 4, - x + y + z = 0, x - 3y + z = 2.

21. If , verify that A² - 4A - 5I = 0. Also find A^-1.

22. Using elementary row transformations,find the inverse of the matrix A =

Continuity and Differentiability :

23. Show that the function f defined as follows, is continuous at x = 2, but not differentiable there at .

24. Find the value of k so that the function f defined by is continuous at x = .

25. If y = and 0 < x < 1, then find the value of .

26. If x = a (cos t + t sin t) and y = a (sin t - cos t), find .

27. Differentiate,

28. Differentiate,

29. Find

30. Find

31. Find

32. If prove that

33. If y = ,prove that

34. If

35. If y = and 0 < x < 1, then find the value of .

36. If x = a (cos t + t sin t) and y = a (sin t - cos t), find .

Applications of Derivatives :

37. A ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2 cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall ?

38. Find the value of c in Rolle's theorem for the function

39. Verify Mean Value Theorem for the function f (x) = (x - 1) (x - 2) (x - 3) in [0, 4].

40. Find the intervals in which the function f given by f (x) = in increasing or decreasing.

41. Show that y = log (1 + x) - , x > - 1 is an increasing function of x throughout its domain.

42. Find the intervals in which the function f given by f (x) = sin x + cos x, , is strictly increas ing or strictly decreasing.

43. Show that the curves x = and xy = k cut at right angles if

44. Show that the condition that the curves should intersect orthogo nally is that

45. Show that the height of the right circular cylinder of maximum volume that can be inscribed in a given right circular cone of height h is

46. Show that the rectangle of maximum area that can be inscribed in a circle of radius r is a square of side

47. Show that the semi-vertical angle of a right circular cone of given total surface area and maximum volume is

48. Show that the right circular cone of least curved surface and given volume has an altitude equal totimes the radius of the base.

49. Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is .

50. Prove that the volume of the largest cone that can be inscribed in a sphere of radius R is of the volume of the sphere.

Integals :

51. Find

52. Evaluate

53. Find

54. Evaluate :

55. Evaluate :

56. Evaluate :

57. Find: .

58. Evalute:

59. Find:

60. Evalute:

61. Evalute :

62. Evaluate

63. Evaluate :

64. Evaluate :

65. Evaluate :

66. Evaluate :

67. Evaluate integrals using limit of sums

68. Evaluate :

69. Evaluate :

70. Evaluate

71. Evaluate

72. Evaluate

73. Evaluate log (sin x) dx

74. Evaluate

75. Prove that

76. Evaluate

Applications of the Integals :

77. Using integration find the area of the region in the first quadrant enclosed by the x-axis, the line x = and the circle x² + y² = 4.

78. Find the area of the region {(x, y) : 0 £ y £ x² + 1, 0 £ y £ x + 1, 0 £ x £ 2}

79. Draw a sketch of the following region and find its area : {(x, y) : x² + y² £ 1 £ x + y}

80. Using integration find the area of the region bounded by the parabola y = x² and the line y = x.

81. Find the area of the region bounded by the parabola y = x² and y = | x |

82. Using integration find the area of the circle x² + y² = 16 exterior to the parabola y² = 6x.

83. Using integeration, find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x² + y² = 32.

84. Find the area of the circle 4x² + 4y² = 9 which is interior to the parabola x² = 4y.

85. Find the area bounded by the curves y = 6x - x² and y = x² - 2x.

Differential Equations :

86. Solve the differential equation (log y - log x + 1).

87. Find the particular solution of the differential equation ; y(e) = e.

88. Find the general solution of the following differential equation :

89. Find the particular solution of the diffrential equation e^x tan y dx + (2 - e^x) sec² dy = 0, given that when x = 0.

90. Solve : (x³ -3xy²) dx = (y³ - 3x²y)dy.

91. Solve the differential equation (1 + y²) (1 + log x) dx + xdy = 0, it being given that y = 1, when x = 1.

Vectors :

92. If are three vectors such that || = 5, || = 12 and , and find the value of .

93. Show that each of the given three vectors is a unitvetor Also show that they are mutually perpendicular to each other.

94. Show that the points A,B,C with position vectors and respectively, are the vertices of a right-angled triangle. Hence find the area of the triangle.

95. If = a, then find the value of the following :

96. Using vectors, find the area of the triangle with vertices A (1, 1, 2), B (2, 3, 5) and C (1, 5, 5).

97. Find a vector of magnitude 6, perpendicular to each of the vectors and where

98. Find the volume of a parallelepiped whose continuous edges are represented by vectors

99. Show that the vectors are coplanar / non-coplanar if are coplanar / non-coplanar.

100. Write the value of

101. Find the value of l, if four points with position vectors and are coplanar.

Three - dimensional Geometry :

102. Show that the angle between any two diagonals of a cube is

103. A line makes angles with the four diagonals of a cube. Prove that

104. Show that the lines x = ay + b, z = cy + d and x = a'y + b', z = c'y + d' are perpendicular to each other, if aa' + cc' +1 = 0.

105. Find the shortest distance between the lines

106. Show that the lines are coplaner. Also find the equation of the plane containing the lines.

107. Find the distance of the point (1, -2, 3) from the plane x - y + z = 5 measured parallel to the line

108. Find the equation of the line passing through the point P (4, 6, 2) and the point of intersection of the line and the plane x + y - z = 8.

109. A variable plane which remains at a constant distance 3p from the origin cuts the coordinate axes at A, B, C. Show that the locus of the centoid of triangle ABC is

110. Find the coordinates of the foot of the perpendicular distance of the point P (3, 2, 1) from the plane 2 x - y + z + 1 = 0. Find also image of the point in the plane.

111. Find the vector equation of the line passing through the point (1, 2, -4) and perpendicular to the two lnes :

112. Show that the lines do not intersect.

113. Find the equation of the plane passing through the intersection of planes 2 x - 4 y + 3 z + 5 = 0, x + y + z = 6 and parallel to the straight line having direction ratios (1, -1, -1).

114. Find the equations of the bisector planes of the angles between the planes 2 x - y + 2 z + 3 = 0 and 3 x - 2y + 6z + 8 = 0 and specify the plane which bisects the acute angle and the plane which bisects the obtuse angle.

115. Find the vector equation of the line passing through (1, 2, 3) and parallel to the planes

116. Find the coordinates of the foot of the perpendicular drawn from the origin to the plane 2x - 3y +4z -6 = 0.

117. Find the values of p so that the lines are at right angles.

Linear Programming :

118. Find graphically, the maximum value of Z = 2x + 5y, subject to constraints given below: 2x + 4y £ 8; 3x +y 6; x + y 4; x 0, y 0

119. Maximize Z = x + 2y

subject to the constraints

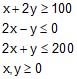
Solve the above LPP graphically.

120. (Manufacturing problem) One kind of cake requires 200 g of flour and 25 g of fat, and another kind of cake requires 100 g of flour and 50 g of fat. Find the maximum number of cakes which can be made from 5 kg of flour and 1 kg of fat assuming that there is no shortage of the other ingredients used in making the cakes. Formulate the above as a linear programming problem and solve graphically.

121. A factory manufactures two types of screws A and B, each type requiring the use of two machines, an automatic and a hand-operated. It takes 4 minutes on the automatic and 6 minutes on the hand-operater machines to manufacture a packet of screws `A' while it takes 6 minutes on the automatic and 3 minutes on the hand-operater machine to manufacture a packet of screws `B'. Each machine is available for at most 4 hours on any day. The manufacture can sell a packet of screws `A' at a profit of 70 paise and screws `B' at a profit of rupee 1. Assuming that he can sell all the screws he manufactures, how many packets of each type should the factory owner produce in a day in order to maximize his profit? Formulate the above LPP and solve it graphically and find the maximum profit?

Probability :

122. The probabilities of A, B, C, solving a problem, are respectively. If all the three try to solve the problem simultaneously, find the probability that exactly one of them can solve the problem.

123. A speaks the truth in 75% cases and B in 80% cases, in what percentage of cases are they likely to contradict each other in stating the same fact?

124. In anewering a question on a multiple choice tes, a student either knows the answer or guesses. Let be the probability that he knows the answer and be the probability that he guesses. Assuming that a student who guesses at the answer will be correct with be correct with probability . What is the probability that the student knows the answer, given that he answered it correctly?

125. Bag I contains 3 red and 4 black balls and bag II contains 4 red and 5 black balls. Two balls are transferred at random from bag I to bag II and then a ball is drawn from bag II. The ball so drawn is found to be red in colour. Find the probability that the transferred balls were both black.

126. A die, whose faces are marked 1, 2, 3 in red and 4, 5, 6 in green, is tossed. Let A be the event "number obtained is even" and B be the event "number obtained is red." Find if A and B are inde pendent events.

127. There are 4 cards numbered 1, 3, 5 and 7, one number on one card two cards are drawn at random without replacement. Let x denote the sum of the numbers on the two drawn cards. Find the mean and variance of X.

128. Suppose that, the reliability of a HIV test is specified as follows :

Of people having HIV 90% of the test detect the disease but 10% go undetected of people free of HIV, 99% of the test are judged HIV negative but 1% are diagnosed as showing HIV positive. From a large population of which only 0.1% have HV, one person is selected at random given the HIV test and the pathologist reports him/her as HIV positive. What is the probability that the person actually has HIV?

129. Uen A contains 1 white, 2 black and 3 red balls ; urn B contains 2 white, 1 black and 1 red ball; and urn C cintains 4 white, 5 black and 3 red balls. One urn is chosen at random and two balls are drawn. These happen to be one white and one red. What is the probability that they come from urn A?

130. A card from a pack of 52 cards is lost. From the remaining cards of the pack, two cards are drawn and are found to be both spades. Find the probability of the lost card being a spade.

131. A random variable X has the following probability distribution :

find (i) k (ii) P (X < 3) (iii) P (X > 6) (iv) P (0 < X < 3).